Background

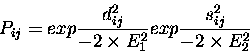
The aim of this work was to provide a set of multiple sequence alignments derived from structure alone. These alignments have obvious uses which have been described elsewhere [1,2]. Numerous other means of deriving such alignments have been presented, but, at the time of the development of STAMP, only one had been applied to alignments of more than two sequences, and no systematic method for assessing the quality of the alignments had been provided. These, then, were the goals of this work.

At the heart of the method is the Argos & Rossmann [3] equation for expressing the probability of equivalence of residue structural equivalence:

$$P_{ij} = exp \frac{d_{ij}^{2}}{-2 \times E_{1}^{2}} exp \frac{s_{ij}^{2}}{-2 \times E_{2}^{2}}$$

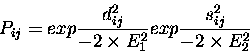
where d_ij is the distance between ${\rm C}_{\alpha}$ atoms for residues iand j, and s_ij is a measure of the local main chain conformation. A detailed description of this equation, and how it has been applied to multiple structures is given in [1].

STAMP makes extensive use of the Smith Waterman (SW) algorithm [4,5,6]. This is a widely used algorithm which allows fast determination of the best path through a matrix containing a numerical measure of the pairwise similarity of each position in one sequence to each position in another sequence. Within STAMP, these similarity values correspond to modified P_ij values (above).

The result of the SW algorithm applied to a matrix of modified P_ijvalues is a list of residue equivalences. From this list, which we may obtain a set of equivalenced ${\rm C}_{\alpha}$ positions. These are used to obtain a best fit transormation and RMS deviation by a least squares method of [7,8]. This transformation can be applied in the relevant way to yield two new sets of coordinates for which calculation (and correction) of P_ij values, the SW path finding and the least squares fitting may be repeated in an iterative fashion until the two sets of coordinates, and the corresponding alignment, converge on a single solution.

This strategy has proved sucessful in the generation of tertiary structure based multiple protein sequence alignment for a wide variety of diverse protein structural families [1,9,10,11,12]. The method can accurately superimpose and obtain alignments for families of proteins as structurally diverse as the greek key $\beta$ sandwich folds (e.g. immunoglobulin domains, CD4, PapD chaperonin, azurin, superoxide dismutase, actinotaxin, prealbumin, etc.), the aspartic proteinase N and C terminal lobes, the Rossmann fold domains, the globin folds (including phycocyanins and colicins), and many others.

It is important to remember that this method assumes overall topological similarity, and will not, without explicit intervention, be able to superimpose/align structures with common secondary structures in similar orientations, but different connectivity or topologies (such as the different types of four helix bundle proteins: up-down-up-down with up-up-down-down).

Two measures of alignment confidence are provided [1]

1. A structural similarity Score (S_c) is defined in order that overall alignment quality and structural similarity may be compared across a wide range of protein structural families. These are defined below.

2. A measure of individual residue accuracy $P_{ij}^{\prime}$ is defined in order that residue equivalences may be normalised with respect to both the number of structures in an alignment and the length of the structures being aligned.

Alignments having a structural similarity Score S_c between 5.5 and 9.8 imply a high degree of structural similarity and almost always suggest a functional and/or evolutionary relationship.. Values between 2.5 and 5.5 correspond to more distantly related structures, and do not always imply a functional or evolutionary relationship. Values less than 2.0 generally indicate little overall structural similarity.

Stretches of three or more aligned positions with $P_{ij}^{\prime}$ values greater than 6.0 generally correspond to genuine topological equivalences, values between 4.0 and 6.0 are equivalent $> 50 \%$ of the time, and values less than 4.0 are generally not equivalent. Stretches of residues having $P_{ij}^{\prime} > 6.0$ generally correspond to regions of conserved secondary structure within a family of structures being compared. For multiple alignments, an alterntaive and more effective way of assessing residue-by-residue equivalence is provided in POSTSTAMP (see below).

Both of these measures are refered to repeatedly below. For a more detailed description of their derivation please refer to [1]. In addition, RMSD is used to refer to the root mean square deviation between atoms selected for a fit. The CUTOFF refers the lowest allowable $P_{ij}^{\prime}$ for the program to use a particular pair of residues in a fit (called `C` in [1]).