



Next: Screening the Results
Up: Materials and Methods
Previous: Additional Details
The speed of the domain scan depends on the size of the segment being
analysed. If the segment contains N residues there are N places at
which a boundary may be placed. A Method 1 scan cuts the segment twice
and so there are 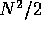 possible splits. A Method 3 scan has
restrictions on where segments may start and end. Suppose it contains
two segments of size
possible splits. A Method 3 scan has
restrictions on where segments may start and end. Suppose it contains
two segments of size 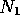 and
and 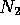 . Each segment is effectively
scanned twice by a single cut. Therefore the speed of the scan can be
given by
. Each segment is effectively
scanned twice by a single cut. Therefore the speed of the scan can be
given by 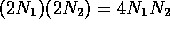 . A Method 2 scan splits the
domain four times and hence its speed varies approximately as
. A Method 2 scan splits the
domain four times and hence its speed varies approximately as
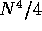 . Restriction on segment sizes helps reduce the number of
combinations, but the algorithm's speed can be increased further in
the following ways.
. Restriction on segment sizes helps reduce the number of
combinations, but the algorithm's speed can be increased further in
the following ways.
Small segments are unlikely to contain two segment
domains. Therefore, a lower bound is placed on the minimum number of
residues in a segment, minimum double split (MDSP). Any single
segment domains with size < MDSP are assumed to contain single
segment domains only. This prevents the algorithm from performing a
two segment scan on the segment and thus saves time.
If the percentage of secondary structure (i.e. helix and
strand) in the domain being scanned is greater than the value given by
sso, the algorithm uses only those contacts to and from secondary
structure elements. Secondary structure element definitions are taken
from the program DSSP [Kabsch & Sander, 1983], using `H' for helix and `E' for strand.
It was found that in cases where only the secondary structure was
used, the maximum split values were generally higher than they would
be had the same domains been scanned using all contacts. To take the
difference in maximum split values into account, the cases in which
only secondary structure contacts are being used are compared against
the variable MSVsso.
While the above restrictions cut down on the number of combinations,
once the actual number of residues being used rises above 250--300, the
algorithm still takes an unreasonably long time to execute. To
circumvent this problem some `pruning' of the search tree is done on
Method 2 scans (see Figure 6b).
The assumption is made that if two segments are correlated,
increasing the size of one segment will not make the segments distinct.
While tree-pruning is successful in most cases, it is not able to
speed up others. In order to speed up all scans the split value is not
calculated at every position for large segments. Instead, the position
of the cutting boundaries is moved by an `increment' skipping over
intervening residues. The increment is calculated by dividing
the size of the segment being analysed by the
increment divider (ID) and adding one. Note that this results in
the cuts corresponding to the maximum split value being over a range
of residues rather than at specific residues. The same situation
occurs when only secondary structure is being considered, as the split
value will remain unchanged as the cut boundary passes over
non-secondary structure residues. In both these cases, once the range
of the the cut boundaries is known the algorithm goes back and
calculates all the split values for all residues in the range using
all contacts. The combination which gives the highest split value is
the one used. Using these methods analysis time was reduced from 11 hours
to 1 minute
on the three domain protein BirA [Wilson et al., 1992] (for a Silicon Graphics Indy
R4000 PC).




Next: Screening the Results
Up: Materials and Methods
Previous: Additional Details
as@bioch.ox.ac.uk
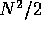 possible splits. A Method 3 scan has
restrictions on where segments may start and end. Suppose it contains
two segments of size
possible splits. A Method 3 scan has
restrictions on where segments may start and end. Suppose it contains
two segments of size 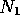 and
and 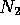 . Each segment is effectively
scanned twice by a single cut. Therefore the speed of the scan can be
given by
. Each segment is effectively
scanned twice by a single cut. Therefore the speed of the scan can be
given by 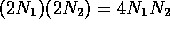 . A Method 2 scan splits the
domain four times and hence its speed varies approximately as
. A Method 2 scan splits the
domain four times and hence its speed varies approximately as
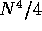 . Restriction on segment sizes helps reduce the number of
combinations, but the algorithm's speed can be increased further in
the following ways.
. Restriction on segment sizes helps reduce the number of
combinations, but the algorithm's speed can be increased further in
the following ways.



