



Although the overall accuracy of an alignment may be estimated from the SD score (see section 4.1) this value does not indicate which regions of the alignment are correct. Experience suggests that the reliable regions of an alignment are those that do not change when small changes are made to the gap-penalty and matrix parameters. An alternative strategy is to examine the sub-optimal alignments of the sequences to find the regions that are shared by sub optimal alignments within a scoring interval of the best alignment. For any two sequences, there usually many alternative alignments with scores similar to the best. These alignments share common regions and it is these regions that are deemed to be the most reliable. For example, the simple alignment of ALLIM with ALLM scoring 2 for identites, 1 for mismatch and -1 for a gap gives:
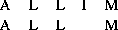
with a score of . The sub optimal alignment:
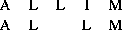
gives a score of but shares the alignment of
AL and M with the optimal alignment. Rather than calculate all
sub-optimal alignments, Vingron and Argos [40] use an elegant and
simple method to identify the reliable regions in an alignment by
calculating the comparison matrix
both forwards and backwards and
summing the two matrices. The cells in
that are equal to
the best score for the alignment delineate the optimal alignment path.
Cells within a selected value of the best score are flagged and
reliable regions defined as those for which there is no other cell
or
with
and
. The results of the analysis
are displayed in the form of a dot-plot with larger dots identifying
the reliable regions.
Although the details of his calculation differ from Vingron and Argos, Zuker [41], produces a dot plot that highlights the regions where there are few alternative local alignments. He also caters for optimal local alignments with gaps. Zuker shows that the alignment of distantly related sequences such as Streptomyces griseus proteinase A and porcine elastase may be clearly seen to be unstable with many sub-optimal alignments close to the optimal.
Rather than use the dot-plot representation, Saqi and Sternberg
[42] directly determine alternative sub-optimal alignments.
They first calculate the matrix and best path, then identify the
cells that contributed to the best path and reduce these by a preset
value (usually 10%of the typical scoring matrix value). A new
matrix is calculated and a new best path and alignment. This process
is repeated iteratively to generate a series of global sub-optimal
alignments.
Investigating sub-optimal alignments by one or more of these methods allows:



