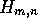 starting with
starting with 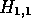 and working forwards through the
matrix column by column. The value of each cell
and working forwards through the
matrix column by column. The value of each cell 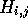 is given by the equation:
is given by the equation:




In order to simplify the explanation of the ``all local alignment'' algorithm I shall first recapitulate a well known method for efficient computer implementation of the Smith-Waterman [Smith & Waterman, 1981] algorithm. For a full introduction to dynamic programming algorithms in sequence comparison see [Kruskal, 1983].
The best score for a local alignment between two sequences
A and B of length m and n is determined by calculating the comparison
matrix 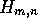 starting with
starting with 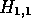 and working forwards through the
matrix column by column. The value of each cell
and working forwards through the
matrix column by column. The value of each cell 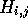 is given by the equation:
is given by the equation:
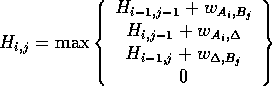
where 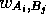 is the score for equivalencing
is the score for equivalencing  and
and
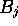 , and
, and 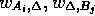 are the scores for
aligning with a gap in B or A respectively. To calculate the
value of
are the scores for
aligning with a gap in B or A respectively. To calculate the
value of 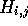 , it is only necessary to know the contents of the
three predecessor cells (
, it is only necessary to know the contents of the
three predecessor cells (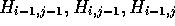 ). If just
the best score is required, and no alignment, then only the previous
column, C of the matrix, need be stored together with the score for
the current cell, r and previous cell, p in the column. This is
illustrated in Figure 1 for the comparison of A =
C-C-A-A-T-C-T-A-C-T-A-C-T-G-C-T-T-G-C-A- G-T-A-C and B =
A-G-T-C-C-G-A-G-G-G-C-T-A-C-T-C-T-A-C-T-G-A- A-C with
). If just
the best score is required, and no alignment, then only the previous
column, C of the matrix, need be stored together with the score for
the current cell, r and previous cell, p in the column. This is
illustrated in Figure 1 for the comparison of A =
C-C-A-A-T-C-T-A-C-T-A-C-T-G-C-T-T-G-C-A- G-T-A-C and B =
A-G-T-C-C-G-A-G-G-G-C-T-A-C-T-C-T-A-C-T-G-A- A-C with 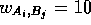 if
if 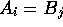 ,
, 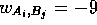 if
if 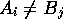 , and
, and 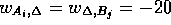 . This example
is used here to allow a direct comparison of the ``all local
alignment'' algorithm with the work of Waterman and Eggert [Waterman & Eggert, 1987].
. This example
is used here to allow a direct comparison of the ``all local
alignment'' algorithm with the work of Waterman and Eggert [Waterman & Eggert, 1987].
Figure 1 illustrates the processing of 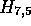 and
and 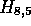 . The
cells of H that are stored are shown in large numerals. The cells
shown in small numerals are discarded. The best overall score is
updated if the value of the current cell is greater than the maximum so far. This
is the simplest efficient implementation of the ``best score only''
local similarity algorithm, and may be coded to run very fast. It is
also straightforward, by the addition of a further 1-dimensional array
to adapt the algorithm to cope with a gap-penalty function having the
form
. The
cells of H that are stored are shown in large numerals. The cells
shown in small numerals are discarded. The best overall score is
updated if the value of the current cell is greater than the maximum so far. This
is the simplest efficient implementation of the ``best score only''
local similarity algorithm, and may be coded to run very fast. It is
also straightforward, by the addition of a further 1-dimensional array
to adapt the algorithm to cope with a gap-penalty function having the
form 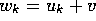 where k is the gap-length [Gotoh, 1982].
where k is the gap-length [Gotoh, 1982].



